Critical Velocity

The velocity distinguishing rolling from freely flowing cells is called critical velocity or hydrodynamic velocity. As a first approximation to determine this critical velocity, a parabolic velocity profile in the microvessel is assumed. Furthermore, a linear approximation is used very near the vessel wall. When cells are at least one cell radius away from the vessel wall, their velocity is the same as that of the fluid, and it can be determined using the equation

vc = h . gw ,

where h is the distance from the wall to the center of the cell, and g is the shear rate. However, due to drag, a freely flowing cell near the wall of the microvessel will have a smaller velocity than the fluid traveling at the same radial position in undisturbed flow (vc < h . gw).

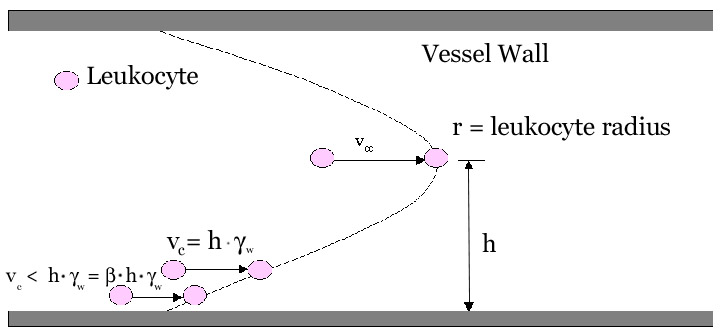
In intravital microscopy experiments, the velocity of a cell flowing in the centerline (vcc) can be determined experimentally. From vcc, the mean blood flow velocity, vB, can be calculated as

vB = vcc/(2 - e2).

Wall shear rate in microvessels is estimated as

gw = 2.12 . 8 . vB / d

where d is the vessel diameter and 2.12 is an empirical correction factor based on velocity profiles measured in vivo (Reneman, 1992). From gw, critical velocity is calculated as

vcrit = b . h . gw

where b is a dimensionless drag coefficient derived from theoretical analysis of a sphere flowing close to a wall (Goldman, 1967). Values of b are listed in a table below. As an approximation, for a clearance (h - r) of about 50 nm, the critical velocity can be estimated as

vcritical = vcc . e . (2 - e)

where e is the ratio of the leukocyte diameter (assumed to be 7mm) to the vessel diameter. Any cell traveling at a velocity below the critical velocity is considered a rolling cell, as it is likely to be retarded by an adhesive interaction with the vessel wall.

Relative distance from cell to wall ((h/r) - 1)

Absolute clearance of cell
(h - r)

Drag factor
b
infinite
infinite
1.00000
9.0677
63.4739 mm
0.99962
2.7622
19.3354 mm
0.99436
1.3524
9.4668 mm
0.97768
0.5431
3.8017 mm
0.92158
0.1276
0.8932 mm
0.76692
0.0453
0.3171 mm
0.65375
0.005004
35.028 nm
0.47861
0.003202
22.414 nm
0.45291

Read the following categorized abstracts or link to Medline to conduct your own query.

  • In vivo study of critical velocity: Endothelial, not hemodynamic differences are responsible for preferential leukocyte rolling in venules.
  • In vitro study of critical velocity: Leukocytes roll on a selectin at physiologic flow rates: distinction from and prerequisite for adhesion through integrins.
  • Goldman AJ, Cox RG, Brenner H. Slow viscous motion of a sphere parallel to a plane wall - II Couette flow. Chemical Engineering Science. 1967;22:653 - 660.
  • Gaehtgens, P, AR Pries, and K Ley. 1987. Structural, hemodynamic and rheological characteristics of blood flow in vivo. In Clinical Hemorheology. S Chien, J Dormandy, E Ernst, and A Matrai, editors. Martinus Nijhoff, Dordrecht, Boston, Lancaster. 97-124.
  • Reneman, RS, B Woldhuis, MGA oude Egbrind, DW Slaff, and GJ Tangelder. 1992. Concentration and velocity profiles of blood cells in the microcirculation. In Advances in cardiovascular engineering. NHC Hwang, VT Turitto, and MRT Yen editors. Plenum Press, New York. 25-40.

Comment on this page's content or view comments made by others!